extra como poner un boton en excel

barra de excel :D

entorno y barra de word :D

La función BUSCARV nos ayuda a buscar un valor dentro de una lista (vertical). La función BUSCARH realizará la búsqueda dentro de un rango de valores horizontal. Para entender mejor la diferencia te mostraré un ejemplo de ambas funciones.

Antes de continuar debemos recordar que la “V” en el nombre de la función BUSCARV significa Vertical y la “H” en la función BUSCARH significa Horizontal.

Búsqueda vertical con BUSCARV

Con la función BUSCARV podemos buscar valores dentro de una columna de nuestra hoja de Excel o de nuestra tabla de datos. En el siguiente ejemplo buscaré el valor “Delta” utilizando la función BUSCARV:

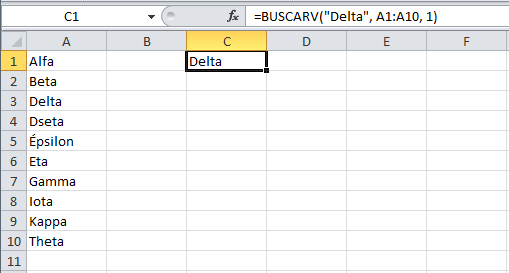
Como puedes observar, el rango de búsqueda es un rango vertical (A1:A10) y es la razón por la que hemos utilizado la función BUSCARV.

Búsqueda horizontal con BUSCARH

Por el contrario, si los datos están contenidos en un rango horizontal, la función BUSCARV no podría encontrar el valor que estamos buscando. La función BUSCARH nos permite hacer este tipo de búsqueda horizontal:

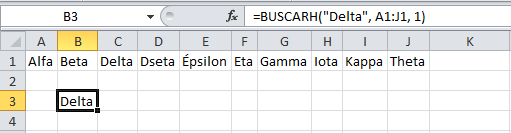
Es muy poco probable, y poco usual, tener datos organizados de manera horizontal por lo que la función BUSCARV es más “famosa” que la función BUSCARH sin embargo es importante saber que Excel nos permite realizar una búsqueda sin importar la manera en que están organizados los datos.

Transponer la matriz de datos

Muchos usuarios de Excel encuentran que la función BUSCARV es más intuitiva o fácil de utilizar por lo que tratan de evitar el uso de la función BUSCARH. Si te encuentras en la situación donde los datos están organizados de manera horizontal, siempre tendrás la opción de transponer la matriz de datos para seguir utilizando la función BUSCARV.

tabla dinamica

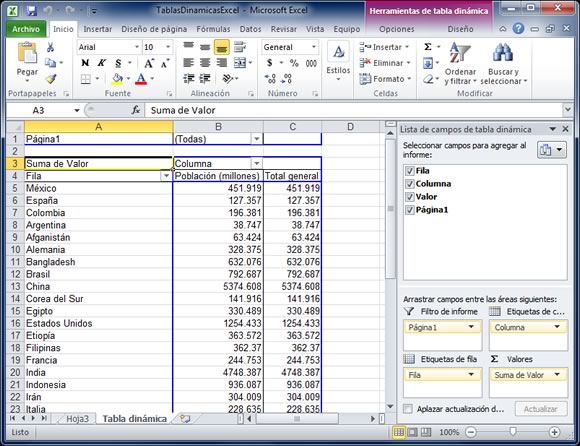
Una tabla dinámica es una de las herramientas más poderosas de Excel, pero también es una de las características que más usuarios de Excel se sienten intimidados a utilizar. Si eres uno de ellos te estás perdiendo de utilizar una gran herramienta de Excel.

Las tablas dinámicas te permiten resumir y analizar fácilmente grandes cantidades de información con tan sólo arrastrar y soltar las diferentes columnas que formarán el reporte.

Reportes flexibles

Es verdad que puedes formar muy buenos reportes con lo que ya sabes de Excel, pero imagina la siguiente situación. Ya has creado un gran reporte que compara el total de ventas en las diferentes regiones del país, pero ahora tus superiores han pedido que hagas otro reporte que compare las ventas de cada región con los tipos de productos vendidos. Y por si fuera poco, después de terminar el segundo reporte, te piden un tercero para comparar las ventas de los productos pero ahora por cada ciudad del país. Es muy probable que tengas que empezar desde cero para crear los nuevos reportes.

Afortunadamente Excel tiene la funcionalidad de tablas dinámicas que ayuda a resolver este problema. Al utilizar una tabla dinámica podrás crear los reportes sin escribir una sola fórmula, pero lo más notable será que podrás arreglar el reporte de una manera dinámica de acuerdo a tus necesidades.

El verdadero problema de las tablas dinámicas

Muchos usuarios de Excel evitan el uso de las tablas dinámicas porque parecieran muy complicadas a primera vista. Aunque las tablas dinámicas pueden parecer desafiantes, la realidad es que el problema radica en que muy pocas veces se explican adecuadamente. En varias ocasiones he leído libros o tutoriales en Internet que utilizan términos como “Análisis multidimensional”, que aunque es un concepto importante, el presentar este tema a un principiante con este lenguaje solo lo intimidará desde un principio.

A partir de hoy iniciaré con una serie de artículos que hablarán sobre tablas dinámicas. Mi objetivo es presentarlas con un lenguaje sencillo de manera que puedas entender fácilmente y pronto puedas utilizar adecuadamente esta característica de Excel que te hará más productivo.

formato condicional :D

El formato condicional resalta rápidamente información importante en una hoja de cálculo. Sin embargo, a veces lasreglas de formato integradas no van lo bastante lejos. La adición de su propia fórmula a una regla de formato condicional le ayudar a agilizar acciones que las reglas integradas no pueden realizar.

Para crear la primera regla:

1. Seleccione de la celda A2 a la A7. Realice esta acción arrastrando desde A2 a A7.
2. A continuación, haga clic en Inicio > Formato condicional > Nueva regla.
3. En el cuadro de diálogoNueva regla de formato, haga clic en Utilizar una fórmula para determinar en qué celdas desea aplicar el formato.
4. En Dar formato a los valores donde esta fórmula sea verdadera, escriba la fórmula: =A2>HOY()
   La fórmula usa la función HOY para ver si las fechas de la columna A son posteriores a hoy (en el futuro). De ser así, se aplica formato a las celdas.
5. Haga clic en Formato.
6. En el cuadro Color, seleccione Rojo. En el cuadro Estilo de fuente, seleccione Negrita.
7. Haga clic en Aceptar hasta que se cierren los cuadros de diálogo.
   El formato se aplica a la columna A.

Para crear la segunda regla:

1. Seleccione las celdas de la C2 a la C7.
2. Repita los pasos 2 a 4 anteriores e introduzca esta fórmula: =C2="Y"
   La fórmula prueba para ver si las celdas de la columna C contienen “Y” (las comillas alrededor de Y indican a Excel que es texto). De ser así, se aplica formato a las celdas.
3. En el cuadro Color, seleccione Blanco. En el cuadro Estilo de fuente, seleccione Negrita.
4. Haga clic en la pestaña Relleno y seleccione Verde.
   El formato se aplica a la columna C.

ENTORNO DE EXCEL

la fabricacion del papiro

ensayo de 600 palabras

BIOGRAFIARAS

precalculo
vitutor
interned

CONCLUCION

la conclucion de nosotros fue buena ya que aprendimos significados jugando en una forma muy dinámica y divertida sobre todo

REPORTE

nuestro equipo entre todos nos apoyamos unos a otros lo cual hicimos un trabajo en equipo muy bueno nos repartimos el trabajo por igual ya que en clase le comenzamos pero lo hicimos demasiado rapido pero lo que pudimos fue avanzar y en horas libre lo terminamos lo cual nos dio un resultado genial y ya en clase definimos unos dellates que teniamos pero todo salio bien

criterio con mis propias palabras

Como sabemos, para memorizar los términos algebraicos tendríamos que estudiar y estudiar varias veces. En este caso no sera así, sera de una manera diferente ya que lo haremos dinámico, es decir, jugaremos al memorama.

1: concepto de termino algebraico. Se llama término a toda expresión algebraica cuyas partes no están separadas por los signos + o -. Así, por ejemplo xy2 es un término algebraico.
 2: concepto de signo. Los términos que van precedidos del signo + se llaman términos positivos, en tanto los términos que van precedidos del signo – se llaman términos negativos.
 3: concepto de coeficiente. Se llama coeficiente al número o letra que se le coloca delante de una cantidad para multiplicarla. El coeficiente indica el número de veces que dicha cantidad debe tomarse como sumando.
 4: concepto de variable. Una variable es la expresión simbólica representativa de un elemento no especificado comprendido en un conjunto.
 5: concepto de un exponente. El exponente de un número muestra cuántas veces el número se va a utilizar en la multiplicación.
 6: concepto de un monomio. es una expresión algebraica en la que se utilizan exponentes naturales de variables literales que constan de un solo término (si hubiera una suma o una resta sería un binomio), un número llamado coeficiente
 7: concepto de un binomio. un binomio consta únicamente de dos términos, separados por un signo de más (+) o de menos (-). En otras palabras, es una expresión algebraica formada por la suma de dos monomios
 8: concepto de trinomio. un trinomio es la suma indicada de tres monomios, es decir, un polinomio con tres términos que no puede simplificarse más
 9: concepto de polinomio. es una expresión matemática constituida por un conjunto finito de variables
 10: concepto de grado respecto a una variable. Es el máximo exponente que posee el monomio sobre la variable; por ejemplo en 2x3 +4x2 + x + 7, el termino es mayor grado es 2x3; este término tiene una potencia tres en la variable x, y por lo tanto se define como grado 3 o de tercer grado
 11: ejemplo de polinomio con más de tres término.

12: concepto de grado absoluto. es el grado máximo de los exponentes de las variables de los monomios que lo componen.
    13: literales utilizadas como constante. Utilizamos la primera letra del alfabeto con constante
 14: conceptos de expresión algebraica. a aquella enunciación, expuesta en lenguaje matemático, formada por números y por símbolos representados por letras
 15: ejemplo de término semejante. x es semejante con 3x ya que ambos términos tienen la misma literal (x).

 17: ejemplo de binomio.

 18: ejemplo de termino que contengas 3 variables y sea de 3 respecto a equis. ax+ax2+ax3
 19: ejemplo de termino que contengan 3 variables y sea de grado 3 respecto a Y. y3+8x+6x2
 20: ejemplo de trinomio .

MEMORAMA ALGEBRAICO

RESULTADOS DEL EJERCICIO 1 OPERACIONES CON NÚMEROS COMPLEJOS

Ejercicio 1. Operaciones con números complejos.

Exercise 1 complex numbers operations from Matematica de Samos

Resultado de la multiplicación con números complejos

resultados de divicion de numero complejo

resuelto raíz cuadrada de números negativos

resultados de la suma y resta de números complejos

fractal 600 palabras

Un fractal es una figura, que puede ser espacial o plana, formada por componentes infinitos. Su principal característica es que su apariencia y la manera en que se distribuye estadísticamente no varía aun cuando se modifique la escala empleada en la observación. Los fractales son, por lo tanto, elementos calificados como semi geométricos (por su irregularidad no pertenecen a la geometría tradicional) que disponen de una estructura esencial que se reitera a distintas escalas. El fractal puede ser creado por el hombre, incluso con intenciones artísticas, aunque también existen estructuras naturales que son fractales (como los copos de nieve). De acuerdo a Mandelbrot, los fractales pueden presentar 3 clases diferentes de auto similitud, lo que significa que las partes tienen la misma estructura que el conjunto total: * Auto similitud exacta, el fractal resulta idéntico a cualquier escala; * cuasiautosimilitud, con el cambio de escala, las copias del conjunto son muy semejantes, pero no idénticas; * auto similitud estadística, el fractal debe tener dimensiones estadísticas o de número que se conserven con la variación de la escala. Las técnicas fractales se utilizan, por ejemplo, para comprimir datos. A través del teorema del collage, es posible encontrar un IFS (sistema de funciones iteradas), que incluye las alteraciones que experimenta una figura completa en cada uno de sus fragmentos auto semejante. Al quedar la información codificada en el IFS, es posible procesar la imagen. Hablamos de música fractal cuando un sonido se genera y se repite de acuerdo con patrones de comportamiento espontáneo que se encuentran con mucha frecuencia en la naturaleza. Cabe mencionar que existen programas informáticos capaces de crear composiciones de este tipo sin intervención del ser humano. A menudo se cita el conjunto de Cantor en relación a los fractales, aunque no es correcto. Su definición, y que suele generar dicha confusión, es la siguiente: se toma un segmento y se lo parte en tres, para luego eliminar el central y repetir dicho accionar infinitamente con los restantes. Un fractal es un objeto geométrico cuya estructura básica, fragmentada o irregular, se repite a diferentes escalas.1 El término fue propuesto por el matemático Benoît Mandelbrot en 1975 y deriva del latín fractus, que significa quebrado o fracturado. Muchas estructuras naturales son de tipo fractal. La propiedad matemática clave de un objeto genuinamente fractal es que su dimensión métrica fractal es un número no entero. Si bien el término "fractal" es reciente, los objetos hoy denominados fractales eran bien conocidos en matemáticas desde principios del siglo XX. Las maneras más comunes de determinar lo que hoy denominamos dimensión fractal fueron establecidas a principios del siglo XX en el seno de la teoría de la medida.Aplicaciones de los fractales: Puede parecer que los fractales son meras curiosidades matemáticas sin ninguna utilidad. Sin embargo son herramientas de gran potencia para afrontar el estudio de fenómenos complejos. Comunicaciones: Modelado del tráfico en redes; Informática: Técnicas de compresión (audio y vídeo); Robótica: Robots Fractales; Infografía: Paisajes fractales; Biología: Crecimiento tejidos, organización celular Evolución de poblaciones Depredador-presa; Matemáticas: Convergencia de métodos numéricos; Música: Composición musical; Física: Transiciones de fase en magnetismo; Química: Agregación por difusión limitada (DLA); Geología: Análisis de patrones sísmicos; Economía: Análisis bursátil y de mercado, fenómenos de erosión, modelos de formaciones geológicas

propiedades de los números imaginarios 200 palabras

Es decir que cuando se eleva al cuadrado o se multiplica por sí mismo, su resultado es negativo. Si se eleva al cuadrado a cualquier otro número real su resultado siempre será positivo. Por ejemplo cinco al cuadrado o 5², es decir 5 × 5 da como resultado 25. En su defecto, -5² a pesar de ser un número negativo su resultado también será positivo debido a que -5 × -5 anula su negatividad y da como resultado 25.Por lo tanto un número potenciado que de resultado negativo solo puede suceder en la imaginación, pero a pesar de parecer imposibles los números complejos e imaginarios son muy útiles y tienen una utilidad real para resolver problemas que de otra manera serían un fracaso. para referirse a lo que hoy en día se conoce como números complejos, el uso común en la actualidad de los números imaginarios significa un número complejo cuya parte real es igual a cero. Para clarificar y evitar confusiones, tales números muchas veces son mejor llamados números imaginarios puros. La suma de los números imaginarios es cerrada, lo cual significa que si se suman dos números imaginarios, el resultado también será un número imaginario.

propiedades de los números reales 200 palabras

Los números reales son los números que se utilizan para la medición de cantidades reales. Incluyen los números racionales, números irracionales, números enteros, decimales, etc. Estas cantidades reales incluyen longitud, velocidad, temperatura ambiente, tasas de crecimiento y muchos más. Los números racionales e irracionales llenan completamente la recta numérica y forman el conjunto de los números reales. En palabras más simples, los números reales se pueden clasificar en números racionales y números irracionales. Estos números racionales se pueden dividir en números enteros y fracciones. Los números reales mantienen algunas de las propiedades básicas de las Matemáticas que por lo general pueden ser articuladas con respecto de las 2 operaciones elementales de multiplicación y suma. Los números reales pueden ser descritos y construidos de varias formas, algunas simples aunque carentes del rigor necesario para los propósitos formales de matemáticas y otras más complejas pero con el rigor necesario para el trabajo matemático formal. Durante los siglos XVI y XVII el cálculo avanzó mucho aunque carecía de una base rigurosa, puesto que en el momento prescindían del rigor y fundamento lógico, tan exigente en los enfoques teóricos de la actualidad.

números irracionales 200 palabras

Los números irracionales tienen como definición que son números que poseen infinitas cifras decimales no periódicas, que por lo tanto no pueden ser expresados como fracciones.En la práctica, para trabajar con números irracionales es preciso utilizar aproximaciones. Estas pueden obtenerse con calculadora, utilizando fórmulas algebraicas o procedimientos geométricos. Los valores obtenidos suelen truncarse o redondearse. Cuando dividimos entre sí dos números naturales, por lo general llegamos a un número exacto, aunque sea después de colocar muchos decimales; pero la operación se cierra, obteniendo como resultado otro número natural. En forma recíproca, ese resultado podemos expresarlo de nuevo como fracción. Sin embargo, existen algunos números que no permiten ser expresados como fracción. Son números cuya cantidad de decimales es infinita, nunca se acaban sus decimales, así es que no se pueden expresar como cociente de dos números naturales. Estos son los llamados números irracionales. No deben confundirse con los números racionales, porque éstos son números decimales finitos, infinitos periódicos e infinitos semiperiódicos que sí pueden transformarse en una fracción, por ejemplo: 18/5 que es igual a 3,6 por lo tanto es un número racional a diferencia de la raíz cuadrada de 2 en cuyo resultado se obtienen infinitos decimales, y su fraccionamiento resulta imposible.

Propiedades de los números racionales 200 palabras

Los números racionales, son el conjunto de números fraccionarios y números enteros representados por medio de fracciones. Este conjunto está situado en la recta real numérica pero a diferencia de los números naturales que son consecutivos, por ejemplo a 4 le sigue 5 y a este a su vez le sigue el 6, y los números negativos cuya consecución se da así, a -9 le sigue -8 y a este a su vez le sigue -7; los números racionales no poseen consecución pues entre cada número racional existen infinitos números que solo podrían ser escritos durante toda la eternidad. Diferencias entre enteros y racional Los números enteros son una generalización del conjunto de números naturales que incluye números negativos (resultados de restar a un número natural otro mayor además del cero). Así los números enteros están formados por un conjunto de enteros positivos que podemos interpretar como los números naturales convencionales, el cero, y un conjunto enteros negativos que son los opuestos de los naturales (éstos pueden ser interpretados como el resultado de restar a 0 un número natural). En sentido amplio se llama número racional o fracción común a todo número que puede representarse como el cociente de dos enteros con denominador distinto de cero; el término "racional" alude a "ración" o parte de un todo, y no al pensamiento o actitud racional, para no confundir este término con un atributo del pensamiento humano.

propiedades de los números enteros 200 palabras

Los enteros con la adición y la multiplicación forman una estructura algebraica llamada anillo. Pueden ser considerados una extensión de los números y un subconjunto de los números racionales (fracciones). Los números enteros son subconjunto de los racionales fracciones, puesto que cada número entero puede ser considerado como una fracción cuyo denominador es el número uno. Los números enteros pueden ser sumados y/o restados, multiplicados y comparados. El conjunto de los números enteros, considerado junto con sus operaciones de adición y multiplicación, tiene una estructura que en matemáticas se denomina anillo; y posee una relación de orden. Los números enteros pueden además construirse a partir de los números naturales mediante equivalencia. El conjunto ℤ de los números enteros es coordinarle con el conjunto ℕ de los números naturales. O sea que se puede establecer un correspondencia biunívoca entre los dos conjuntos. Al igual que los números naturales, los números enteros pueden sumarse, restarse, multiplicarse y dividirse, de forma similar a los primeros. Sin embargo, en el caso de los enteros es necesario calcular también el signo del resultado.

propiedades de los números naturales 200 palabras

Entre los números naturales están definidas las operaciones adición y multiplicación. Además, el resultado de sumar o de multiplicar dos números naturales es también un número natural, por lo que se dice que son operaciones internas. La sustracción, sin embargo, no es una operación interna en N, pues la diferencia de dos números naturales puede no ser un número natural (no lo es cuando el sustraendo es mayor que el minuendo). Por eso se crea el conjunto Z de los números enteros, en el que se puede restar un número de otro, cualesquiera que sean éstos. Los números naturales son los primeros que surgen en las distintas civilizaciones, ya que las tareas de contar y de ordenar son las más elementales que se pueden realizar en el tratamiento de las cantidades. La división tampoco es una operación interna en N, pues el cociente de dos números naturales puede no ser un número natural (no lo es cuando el dividendo no es múltiplo del divisor). Por eso se crea el conjunto Q de los números racionales, en el que se puede dividir cualquier número por otro (salvo por el cero). La división entera es un tipo de división peculiar de los números naturales en la que además de un cociente se obtiene un resto

SISTEMAS DE NUMERACIÓN NO POSICIONALES 400 palabras

Estos son los más antiguos, se usaban por ejemplo los dedos de la mano para representar la cantidad cinco y después se hablaba de cuántas manos se tenía. También se sabe que se usaba cuerdas con nudos para representar cantidad. Tiene mucho que ver con la coordinabilidad entre conjuntos. Entre ellos están los sistemas del antiguo Egipto, el sistema de numeración romana, y los usados en Mesoamérica por mayas, aztecas y otros pueblos. Al igual que otras civilizaciones mesoamericanas, los mayas utilizaban un sistema de numeración de raíz mixta de base 20 (vigesimal). También los mayas preclásicos desarrollaron independientemente el concepto de cero (existen inscripciones datadas hacia el año 36 a. C. que así lo atestiguan.). En los sistemas no posicionales, los dígitos tienen el valor del símbolo utilizado, que no depende de la posición que ocupan en el número. En estos sistemas, aunque se prefería un orden de representación, los dígitos podían aparecer en cualquier posición. Entre los sistemas de numeración no posicional se encuentra el egipcio. El sistema de numeración egipcio era decimal y no posicional. Cada unidad se representaba con un trazo vertical; las decenas, con un arco, y las centenas, millares, decenas de millar, centenas de millar y millones, con un jeroglífico específico. Observa los siguientes ejemplos y comprueba que el valor es el mismo en ambos casos. SISTEMAS DE NUMERACIÓN SEMI-POSICIONALES Estos sistemas no son estrictamente posicionales y algunos de los símbolos tienen el mismo valor en distinta posición. Entre estos sistemas de numeración se encuentra el romano. El sistema de numeración romana se utilizó en los territorios romanos y aún se sigue usando para indicar los siglos, para representar el mes en la expresión abreviada… Símbolos I V X L C D M Valor decimal 1 5 10 50 100 500 1000 SISTEMAS DE NUMERACIÓN POSICIONAL En estos sistemas la posición de cada dígito determina su valor tanto globalmente como individualmente. Nuestro sistema de numeración es posicional. Veamos un ejemplo: 375 → 3 centenas = 300 unidades 213 → 3 unidades = 3 unidades

Origen de los números 600 palabras

Hace unos 6000 años a.c. los fenicios, sumerios y babilonios registraban sus hechos y acontecimientos por medio de figuras dibujadas en arcilla húmeda, este tipo de escritura se llamó cuneiforme, o en forma de cuña, porque cada trazo del escrito se hacía oprimiendo sobre tablillas de arcilla que posteriormente secaban al sol o la cocían. El trazo representaba el objeto dibujado, posteriormente lo convirtió en un símbolo relacionado con el mismo objeto, esta etapa de la escritura que el hombre desarrolló, se le llamó ideográfica. Los egipcios emplearon una escritura ideográfica que se fue perfeccionando con el tiempo y recibió el nombre de jeroglífica, este modo de escritura les servía para realizar sus inscripciones en los templos, tumbas y monumentos. La escritura ideográfica egipcia tiene dos evoluciones perfectamente definidas, la primera parte de la evolución de la escritura ideográfica es convertirse en jeroglífica para acabar en una escritura cursiva con sus dos variedades, la hierática y demótica. La escritura hierática era una especie de taquigrafía abreviada de los jeroglíficos, muy usada entre los sacerdotes para expresarse rápidamente al no utilizarse el dibujo, cada jeroglífico tenía su correspondiente abreviatura hierática, dominando el elemento fonético y escribiéndose de derecha a izquierda. Antes de existir el lenguaje escrito, el hombre primitivo se comunicaba con sus semejantes gesticulando palabras o sonidos, este medio de lenguaje audible se fue perfeccionando al cabo de miles de años de su continuo uso, hasta llegar a la palabra hablada. Cuando éste deseaba recordar un hecho o transmitir un acontecimiento a sus congéneres, les comunicaba sus ideas por medio de la pictografía. Esta consistía en representar por medio de objetos lo que se deseaba expresar ayudado del dibujo o la pintura, de esta manera el hombre inventó su primera forma de comunicación no hablada, la escritura pictográfica. Aunque se carece de información fidedigna acerca de la forma como el hombre primitivo empezó a valerse de un sistema numérico, tuvo muchas razones y situaciones cotidianas que lo impulsaron a tratar de cuantificar todo lo que le rodeaba. En su etapa sedentaria se vio forzado a emplear algún método de conteo, ya fuera para saber cuántas cabezas de ganado u ovejas poseía; como también para conocer el número de armas que tenía, o para cuantificar la extensión de los terrenos sembrados o conquistados. De esta manera el hombre descubrió el primer sistema de matemáticas aplicadas, que luego los matemáticos definirían como una correspondencia biunívoca entre dos órdenes. Al tener el hombre antiguo un sistema base de medida, se vio en la necesidad de cuantificar las medidas en su modo base de contar, esta operación la llevó a cabo, por ejemplo, utilizando un sistema de rayas rasgadas en las paredes o pintadas en papiro. Otro método era haciendo marcas en los troncos de los árboles o cortes sobre una vara para llevar un registro permanente de las cosas. Cada pueblo o tribu tuvo que inventar sus propias palabras y signos para representar sus operaciones de conteos realizados, con el comercio los antiguos mercaderes estaban obligados a saber una gran variedad de sistemas de medidas y numeración, a fin de poder comerciar con los diferentes pueblos o tribus. Para llegar a la concepción e invención de un sistema numérico, fueron necesarios muchos miles de años antes que el hombre concibiera la idea del número, la invención de un sistema numérico es quizá una de las mayores invenciones del hombre antiguo. Dentro de estos sistemas se encuentran los aditivos, los híbridos y los posicionales. El primer sistema de numeración griego se desarrolló hacia el 600 A.C. Era un sistema de base decimal que usaba los símbolos de la figura siguiente para representar esas cantidades. Se utilizaban tantas de ellas como fuera necesario según el principio de las numeraciones aditivas.

Los números complejos.

Complex numbers from Matematica de Samos

300 palabras :D El profesor y el alumno

Muchas de la veces pensamos que tenemos la vida resuelta, pero la realidad es otra, estamos acostumbrado o nos a malacostumbrado a que ellos nos dicen todo, y la tecnología nos ayuda bastante pero no la sabemos usar El hecho de que la clase sea colectiva no menoscaba la individuación concreta, porque el esfuerzo radical del profesor se encamina a descubrir, bajo lo común y general, lo propio y particular de cada educando. En cambio, la relación del discípulo con el maestro (de ‘vuelta’) no realiza el esquema de amistad puesto que el alumno no busca esencialmente el hombre concreto que hay debajo del maestro. La actitud del alumno, por el contrario, tiende a mantener con el docente un tipo de relación puramente profesional y externa. Cada alumno aporta a la relación su propio marco de referencia, su manera de ser, su intimidad, sus necesidades, emociones y prejuicios, que influyen en sus comportamientos y respuestas. La relación profesor-alumno que se establece no es gratuita de entrada. Al comienzo se basa en la apreciación de papeles establecidos que con la continuidad se delimitan, se precisan y consolidan. La función del docente contiene más funciones y es más amplia: instruye, estimula, corrige, forma y orienta. Cuando el docente es íntegro conoce su materia, es cálidamente exigente por ser ejemplar, logra el afecto y la admiración de sus alumnos. Su prestigio mueve al alumno a responder con respeto, atención e interés por su curso. Es una relación -bipolar de ida y vuelta- que se establece entre personas de diferente edad y grado de madurez. A la intensidad, variedad e irracionalidad de las reacciones, de los comportamientos, de las actitudes y de las motivaciones de los alumnos, el profesor debe responder con paciencia, ecuanimidad, prudencia y exigencia en su actuar, en sus juicios y en las manifestaciones de su carácter.

Ley de Bode-Números reales y notación científica. Ejercicio 1 (contestado)